The problem “Boat in the River” is proposed by Dan Mayer in his blog dy/dan.
For the first twenty-three seconds I was confused. There was nothing which was out of the ordinary and nothing to solve. Everything was normal until the twenty-three second mark. Then the hook sank. Dan resets the camera, approaches the down escalator and launches himself up the down escalator.
I particularly love this problem because it requires no set up and no explanation. There is simply inquiry, maybe perplexity. By the end of the movie I was naturally drawn to the question of “How long will it take Dan to run up the down escalator?” Although this isn’t the only problem I can think of, it is the main one I am drawn to. Perhaps we could ask: If Dan were to stand on the escalator would it be faster for him to take the stairs? Is running down the stairs faster than running up the stairs? Or: how quickly is Dan running? Something I enjoy about this problem is that we get to create our own question.

After choosing which question to solve I quickly realized that I would need to collect some information from the movie. For the next twenty minutes or so I played around with the movie, watching it over and over, counting steps, watching the timer, and writing down my observations. Above you can see the results. I organized my data into a table with three columns. For the first column I played the movie over 4 times, each time I watched a different runner and guessed at the time when Dan hit the end of the stairs. Column two was created only after I remembered that I could pause the movie and column three was not added until later on. With all this information I made some immediate conclusions:

Which I struggled to explain.

I even made some incorrect assumptions.
Even though I thought I was asking the right question I was not answering my questions correctly. I assumed that Dan was giving us a lot more information than he actually was. The unfortunate assumption was made that the speed that Dan walked down the stairs was equal to the rate of descent. I attempted to barrel forward into the depths of the problem and was immediately stumped. I could not think of any way to solve the problem without calculating speeds and distances.
My pondering led me to the third column. I went back to the movie to collect more information, namely the number of steps that Dan took to reach the end of the stairs in each case, and added the results to column three of my table. This new data did not spur me into speed and velocity mode right away though. This new data lead me to what I thought might be a new way to solve the problems I was asking. If I could figure out how many steps Dan had to climb up to reach the top of the down escalator then I could figure out approximately how long it would take to climb the escalator.
So I drew a picture:
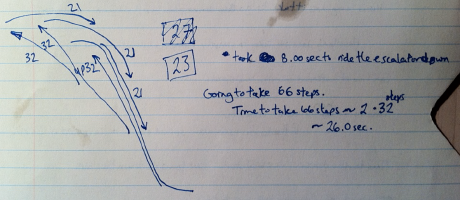
Although my logic was sound, I felt that this technique shouldn’t have worked with the information I was using. The only reason it did was the numbers were relative and the ratios between the two were approximately correct. If Dan were to take 32 steps up the escalator how far would the escalator take him down?
Turns out if you watch the video, keep track of the escalator step that Dan steps on first, pause the movie when Dan reaches the bottom of the stairs, and count the stairs back up to the top from that original step you can calculate the speed of the escalator. There was 21 steps back to the top of the escalator. So for each 32 steps that Dan takes he gains 11 steps up the escalator. If we do this three times we see that Dan can reach the top within sixty-six steps. My calculation for time became very approximate at this point. If it takes thirteen seconds to walk 32 steps it would take approximately 26 seconds to walk up the 66 steps to the top of the escalator.
The number I had used to find this answer was not the number of steps the escalator moved but rather the number of steps Dan took to get to the bottom of the escalator which just so happened to be 21. Dissatisfied with my solution I proceeded to search for another way of solving this problem. I started to calculate speeds using the data I had collected and began to introduce symbols.

Symbols which served only to to confuse me when I tried to use them.

At this point I became thoroughly overwhelmed with information. The numbers seemed to be telling me that I would not be able to walk up the down escalator, which didn’t make any sense. If I started at the bottom of an escalator and my step rate was not sufficiently fast enough then I could not climb the escalator backwards. This was also the point at which I realized that I could not possibly be correct in the assumption that Dan was walking down the stairs at the same speed that the escalator descended. I went back to interpret exactly what the speeds I had calculated meant.

Finally a breakthrough. I realized that to calculate the speed of each trip I would need to use the distance up the escalator, not the number of steps involved with each trip. Since the distance was a constant and each of the trips were relative to each other I also realized that I did not have to measure the distance up the escalator. I used the value of one distance to calculate the speed based on distances up the escalator per second.
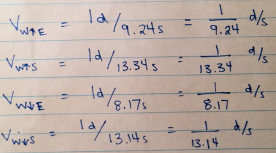
Using this information I could easily calculate the solution to the problem.

Completely satisfied that I was correct I proceeded to watch the solution video:
Turns out the answer is 23 seconds. Not bad for all the estimating I had to do. Was I successful? I guess that would depend on what I defined as successful in mathematics, which in turn would depend on what I defined success in mathematics as.
Could successful mathematizing mean the evolution of a problem? Could it mean creating a question, discussing what is important, describing how we collect information, and trying to decipher what that information means? Could it include taking short cuts and making mistake? When we take a short cut might we discover a new way of thinking that lets us see things in new light? Might making a mistakes force us to think about where we went wrong? Might it include testing our theories in the real world and reflecting on why we may have arrived at a different conclusion? Might it include creating new information from old information and calling on past experiences? Might we allow the dynamics of a problem to contributes to our growth?
Then considering this, successful mathematizing might include asking problems that challenge and perplex us. Success might envelope asking questions like “How fast is Dan walking?” and collecting the information that we need to answer that question. It might includes describing what is going on in a picture, or a movie. We might encounter dead ends and have to erase our work. And to answer my previous question about success, I propose that even if I had not reached a solution, nay, had I not even stepped past the collection of data that this problem requires I might still have participated in successful mathematizing.




