This investigation involves observing the rates of change of different rotating, swinging, falling, and speeding objects using video technology to create data, observations, and analyses. The portfolios might include observations, measurements, calculations, and tentative conclusions in the form of pictures, movies, and text.
Some scenarios that might be used to demonstrate observed rates of angular change are:
- A swing.
- A slide.
- Someone running.
- Something falling.
- Something being thrown.
Think about depicting a situation where the angular rate of change is constant.
Think about depicting a situation where angular rate of change is NOT constant. (ie. the angular speed is changing.)
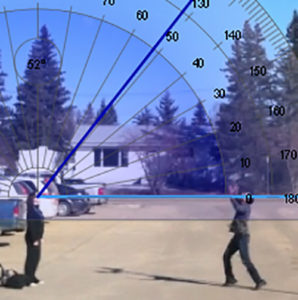
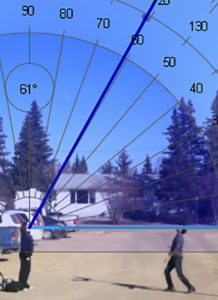
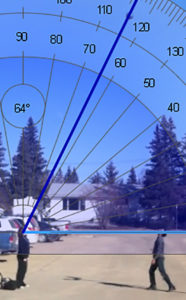
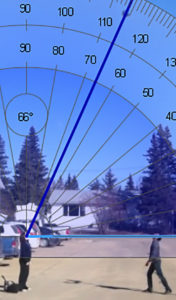
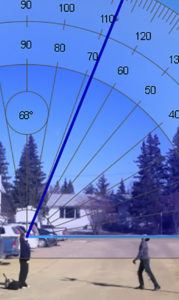
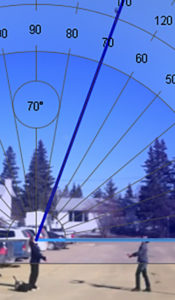
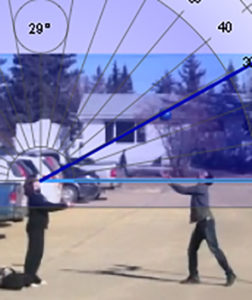
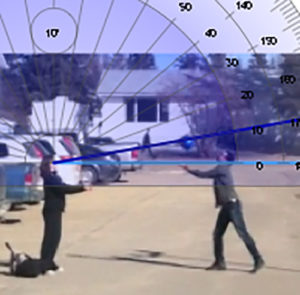
A series of screenshots from a video at evenly spaced increments can be used to capture an accurate image of what is happening during the video.
Data can then be collected from the each screenshot by measuring angles, distances, or other observable phenomenon.
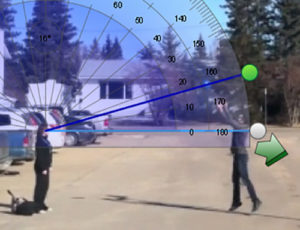
Ex. If I throw a ball into the air. I will measure the angle of elevation from an observer and I will record the height of the ball.
Use your plotted data to calculate the rate of change in each of the scenarios.
Interpret the data you’ve collected.
Extension: Propose one situation where angular speed would only get faster and faster, and one situation where angular speed would only get slower and slower.
Exemplar
Observing a Passing Object
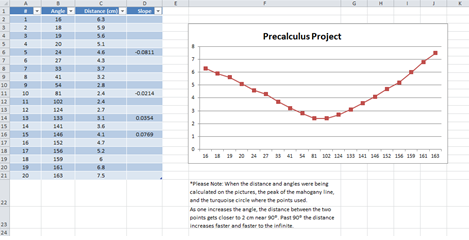
Exemplar
Throwing a Ball in the Air
This project is about how quickly the viewing angle changes as the height of the ball changes after I throw it in the air. By measuring the height with respect to the angle I can figure out the angular rate of change.
When I plotted the Distance vs. Degrees I discovered that the ball has to travel further at the top of its peak than at the bottom in order to change the angle of observation by the same amount.
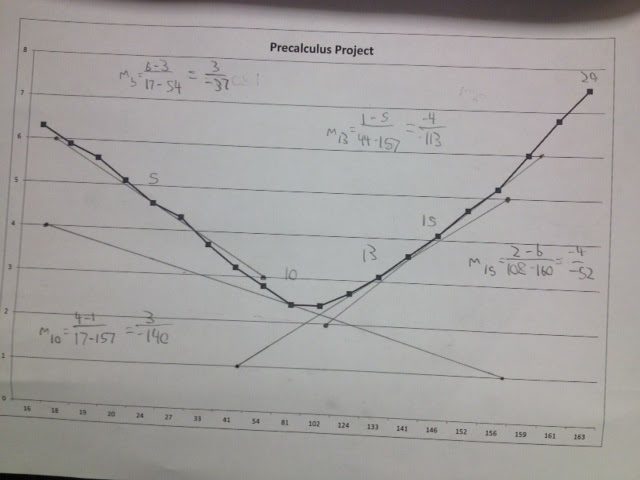
Exemplar
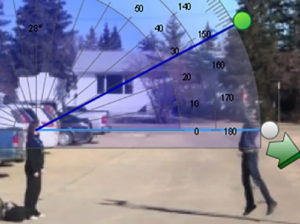
Gravity’s Effect on a Ball

You can see by this graph that as the ball speeds upwards, it loses it’s velocity and slows down. At the top it hits a standstill at 0 m/s. When it comes down it gains speed until it hits the ground and bounces. I deduce that gravity IS a factor. Voila.
Exemplar
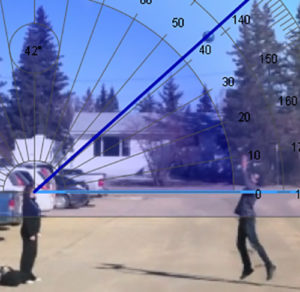
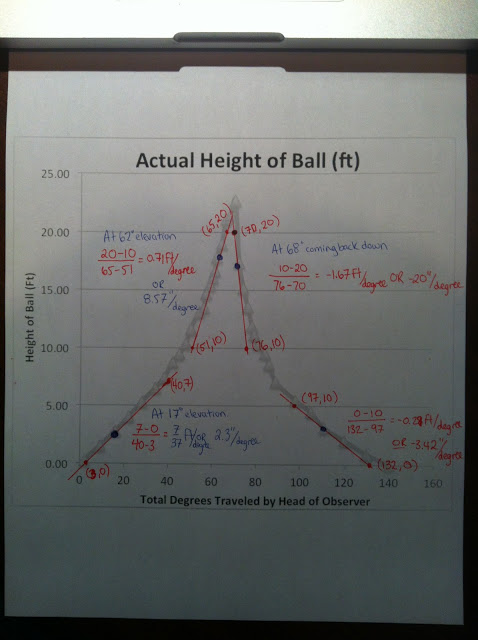
The Viewer’s Head Movement

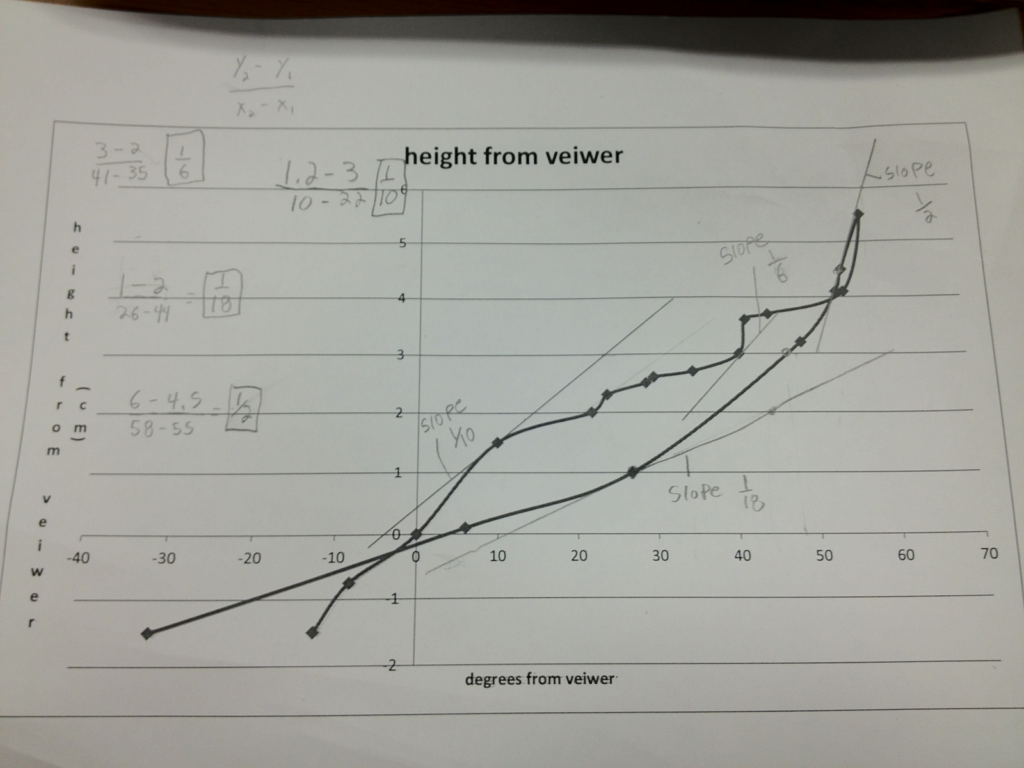
The ball speeds up at the beginning and slows down when it is close to the top. After it reaches the top, it speeds up againg until it hits the floor. as the ball begins to reach its maxamum the veiwer does not have to move his head as far up from angular rate of change, and vice versa for is minimum.
Exemplar
The Angle of Observation

Exemplar
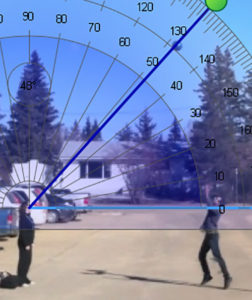
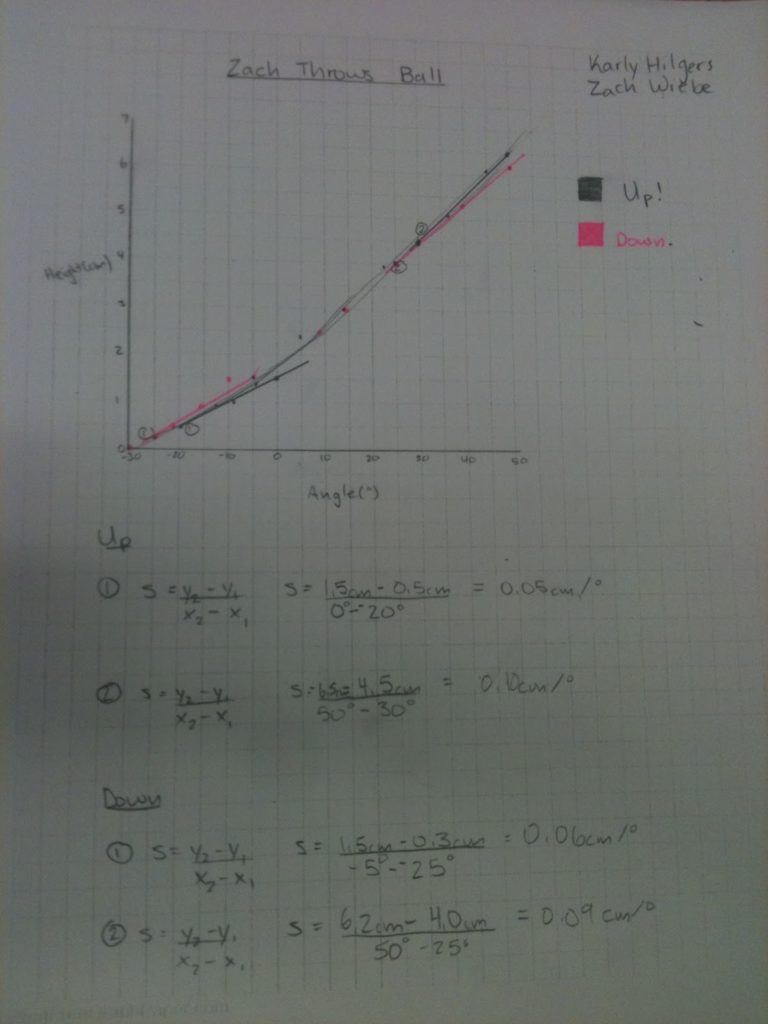
Watching a Thrown Ball
The ball went up at rest. It quickly accelerates to maximum speed then it decelerate to 0 m/s when it reach its maximum height. As it comes down, it accelerates again close to maximum speed until it hit the ground.
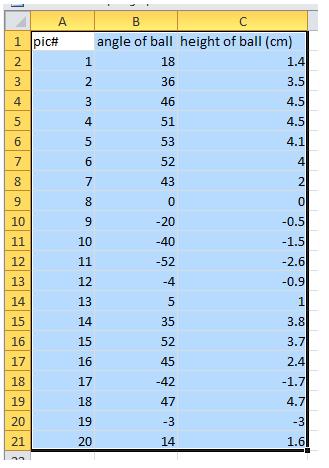
The ball remains going at a constant maximum speed regardless of height.
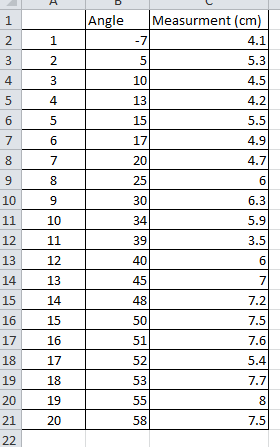
Data collected from the throw video (note: not in chronological order).