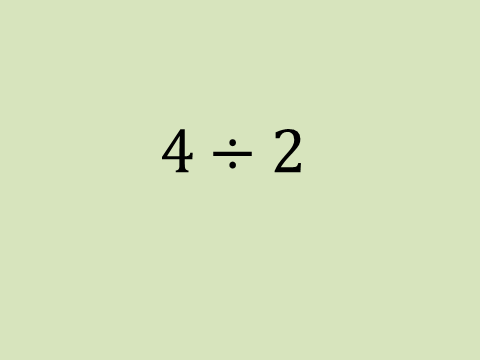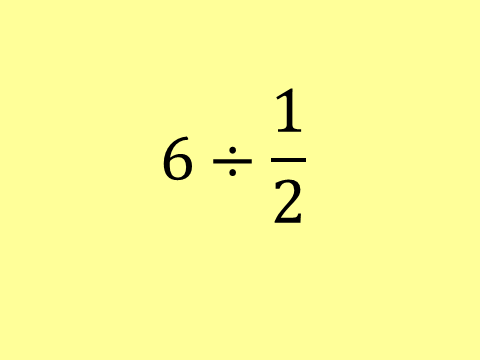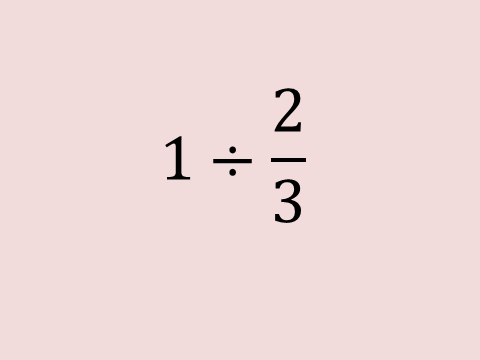Abstract
Nelson Education published a textbook recently for the Knowledge and Employability Mathematics program. It is sold to teachers as a resource “written at an appropriate reading level” that “supports 100% of the outcomes in the curriculum” (Brydon et al,. 2011c). Close examination of this resource reveals assumptions and instructions that undermine the purposes of the curriculum and create intellectual barriers that could stifle the development of students as creative thinkers and responsible, contributing members of society. This paper critiques the resource for its tendency to glance over curriculum outcomes and emphasize procedural solutions over mathematical processes. However, I admit that instructors who use this resource are not doomed to failure; the resource is not a complete write off. We can create lessons from this resource that promote mathematical processes and develop critical thinking by examining the contributions of the individual exercises and creating specific sequences of tasks that reflect the curriculum values.
Keywords: curriculum, division of fractions, mathematics, knowledge and employability, nelson education, program of studies
The Division of Fractions
Introduction
Textbook publishers take advantage of overworked instructors who acquire textbooks as a means of reducing workload. A few examples on a whiteboard, a video that can be replayed, and several pages of contrived, monotonous tasks are sold to educators as formulas that will lead students to success regardless of their academic standing (Brydon et al., 2011a). Students are expected to memorize these procedures, practicing them over and over until they can confidently recite the script verbatim as though they were participating in a theater production. Thankfully, many teachers have assumed the mantle of professionalism despite the demands placed upon them by commercial institutions. They strive to challenge their pupils by acknowledging the power of appropriate tasks, recognizing student contributions when making curriculum decisions, and pushing each learner to a place of independence and functionality (Cirillo et al., 2009). Further, responsible instructors recognize the curriculum as it is interpreted by textbook publishers does not necessarily reflect the philosophy and rationale of the legislated curriculum (Alberta Education, 2017; Cirillo et al., 2009). This paper examines resources that educational publishers have provided for the Knowledge and Employability program and provides reasonable alterations and alternatives that are supported by mathematics education research.
Nelson Education: Mathematics for Apprenticeship and Workplace 10.
Students who have not met the requirements of the demanding tenth grade mathematics program of studies and those students who have been appropriately streamed are given the opportunity to prepare themselves for their transition to the workplace in the Knowledge and Employability program. Instructors teaching this program are obliged to provide practical and applied learning opportunities in combination with teaching a curriculum filled with mathematical competencies and processes (Alberta Education, 2017). This program intends to close gaps in learning for students who have not encountered ideas and concepts such as numeracy, measurement, and statistics. For example, the division of fractions is not encountered until eighth grade and for students who have historically struggled with mathematics this course is an opportunity to revisit these ideas (Alberta Education, 2017).
Nelson Education (2011a) provides a resource that combines learning objectives from grades three to eight in short, six-page lessons. The resource provides matter of fact explanations delivered with the authority of the mathematics community using statements such as “to divide two fractions” and rationalizing these approaches by presenting their preferred methods as “usually easier” (Brydon et al., 2011a , p. 67; Morgan, 1996). The authors pitch their procedures as reliable while at the same time casually admitting that there are other less efficient, fickle methods of approaching the problems (Brydon et al., 2011a; Morgan, 1996). The resource acknowledges alternative ways of thinking, pictorially, only once and that solution is closely followed by exactly how the problem could have been solved using the approved method (Brydon et al., 2011a). There are no other authoritative solutions presented to learners and even the one that is presented is done so using a sidebar and described as unnecessary by using phrases such as “can mean” (Brydon et al., 2011a , p. 67; Morgan, 1996). Interpretive considerations act as secondary sources of information belonging in corollaries and trailed by more appropriate procedural solutions (Morgan, 1996). Students would not accomplish the goals of the curriculum under the direction of the Knowledge and Employability program of studies using this resource as it is presented (Alberta Education, 2017).
Encountering progression within this resource is nearly impossible. The authors provide a mash up of problems that, in one lesson, vaguely resemble scenarios that have the potential to be solved using operations on fractions. They attempt to address the addition, subtraction, multiplication, and division of fractions in six pages by providing fill in the blank explanations and half completed solutions resembling ciphers that students are required to decode. Rules such as ‘invert and multiply’ dominate the lesson plans, worksheets, and solution manuals and would no doubt monopolize the conversations of those classrooms brave enough to use this resource (Brydon et al., 2011a). It is difficult to understand whether the authors of this resource are neglectful, purposefully overlooking the value of conceptual learning in favor of procedural fluency, or if they genuinely don’t understand the concepts themselves and are predisposed to omitting opportunities for conceptual learning. Assuming that a professional could unwind this poorly constructed series of disconnected tasks they might be able to reassemble a lesson of value from the broken pieces (Davis, 2001). The following is an analysis of several problems in the order they appear in the resource concerning the division of fractions.
Discussion of tasks
Calculate. Express the result in simplest terms.
The authors don’t bother introducing division to their pupils, instead they cut to the chase; multiplication by the reciprocal being their preferred manner of practice (Brydon et al., 2011a; Henningsen & Stein, 1997). They provide a perfect opportunity for real learning, 5/8 ÷ 1/8, and then proceed directly into what I can only describe as a completely unnecessary procedural routine (Brydon et al., 2011a). It’s as though they’ve sent this problem to a proverbial slaughterhouse to be butchered. While the original task invites student response and inventiveness, the task declines into mundanity upon the authors needless insistence that we standardize solutions and in doing so they prevent students from encountering meaningful representations of the problem and introduce superfluous numerical complexities.
If a student were to attempt to follow the recommended series of steps, none of which are necessary to solve the problem, the task would devolve from an intellectual thought experiment to a drawl word search meant to curry favour from the instructor (Henningsen & Stein, 1997). The authors might as well replace this activity with the New York Times Sunday Edition crossword puzzle if they are unwilling to provide some semblance of justification for the actions they expect from their students; especially if they expect students to follow a strictly procedural solution. As professionals guiding students through the curriculum we also need to question the reasonableness of asking a student registered in the knowledge and employability program to analyze a sequence of arbitrary, hollow instructions and to transfer the processes to unique scenarios (Henningsen & Stein, 1997). The young adults registered in this course function between a third and a sixth grade mathematical level with low resilience and a high occurrence of learning disabilities (Alberta Education, 2017). To expect them to succeed while interpreting tasks such as 1/2 ÷ 3/4 or 2 3/4 ÷ 1 1/2 without first visualizing a fitting context defies rationality and is inconsistent with Alberta Education’s expectations (Alberta Education, 2017; Brydon et al., 2011a).
Humphreys (2005) approaches a similar task in her classroom by reintroducing the concept of division and then challenging students with more difficult problems. Her lesson begins by acknowledging student competence using problems such as 6 ÷ 1/2 and then proceeds to challenge her students with more conceptually difficult tasks (Boaler & Humphreys, 2005; Sullivan, Clarke, & Clarke, 2009). Her final task, 1 ÷ 2/3, imitates those found in the Nelson Education resource; it is not difficult to solve nor is there anything extraordinary about it (Boaler & Humphreys, 2005). However, her students find greater success since all of her tasks include deciding what they think the answer is and then trying to prove that their answer makes sense (Boaler & Humphreys, 2005). Her students are required to defend their explanations against peer review and detect faults in other students’ solutions (Boaler & Humphreys, 2005). Catherine requires students to persuade themselves, collaborate with their friends, and critique any insufficiently convincing arguments presented by other classmates (Boaler & Humphreys, 2005). This straight forward instructional approach invites every student to participate in the presentation of solutions using different roles. Those “students who did not understand something could place the burden on whoever was explaining to do so clearly” (Boaler & Humphreys, 2005, p. 41). Her students are not made to feel inadequate when they fail to provide an adequate or correct solution; instead they are commended for their efforts and applauded for their contribution to the mathematical community (Boaler & Humphreys, 2005).
Aden is a baker.
The intimidating amount of text used the authors use to describe their recommended solution to this problem offsets the value that this problem adds to their sequence of tasks. The recommended solution seems to avoid engaging with any real practicality introduced through the context by steering students towards the recommended processes using impractical questioning (Brydon et al., 2011a). In this example, the authors place more value on the procedures that students can memorize rather than on anything appearing in the front matter of the curriculum (Brydon et al., 2011a). They neglect the opportunities that this task provides for students to make decisions, think creatively, work as a team, and pose problems. There is a completely unnecessary “hint” provided in the sidebar that further compounds their investment into their one size fits all solution (Brydon et al., 2011a , p. 69). As it is presented, this task fails to address mathematical processes from communication to visualization in meaningful ways (Alberta Education, 2017; Henningsen & Stein, 1997). Like a gambler betting on a losing race horse, Nelson Education continues to throw their money towards a procedure that can accomplish the task without accounting for the existence of more elegant solutions that humans are capable of. Students could have the opportunity to relate the various mathematical strands to each other were this same problem presented in a more suitable manner (Alberta Education, 2017). A student could choose to create a pictorial representation of the cinnamon roll or create a multiplication or addition equation, others might choose to analyze the context using imperial measurement, and still more might approach the problem concretely using an empty cardboard roll.
Dan Meyer (2014), a mathematics educator from the United States, creates similar tasks for his students. He suggests approaching these tasks by first inviting students to participate in the creation of mathematical problems, acknowledging that mathematical inquiry begins by piquing the curiosity of mathematical investigators (Meyer, 2014). I suggest that instructors can further increase the activities breadth by supplying students with measuring cups marked with imperial measurements and requiring them to collect their own experimental data that roughly approximates the volume of the containers (Sullivan et al., 2009). Doing so will launch the activity concretely rather than pictorially and encourage conversations regarding reasonableness and approximation (Alberta Education, 2017). Containers labelled with imperial units can steer the direction of the lesson towards fractions and immerse students pictorially and symbolically within the appropriate curriculum objectives (Alberta Education, 2017). A large variety of measurements combined with low precision and poor student assumptions can lead to a variety of representations of the task and rich mathematical conversations that have the potential to develop the students understanding of fractions and operation on fractions (Alberta Education, 2017; Davis, 2001).
Kelsey has three jars of paint.
Accessible problems are rare within this resource; this problem is accessible and even has an image to complement it (Brydon et al., 2011a). It encourages students to think about fractions pictorially and offers them an opportunity to examine how volumes of different sizes can be represented by the same numerical values. Students asked to complete this activity could engage in creative thinking and demonstrate their mathematical literacy by completing this activity without using any prescribed procedures; realizing the goals of the curriculum effortlessly (Alberta Education, 2017). However, a closer look through the solution manual reveals ulterior motives.

The solution manual ignores suggestions from the curriculum such as developing teamwork skills, fostering the ability to make accurate estimations, and selecting appropriate solution strategies (Alberta Education, 2017; Brydon et al., 2011b). What could have been solved with pencil crayons and critical thought becomes a platform to sell students the authors recommended procedure.
I can only hope that reasonable instructors have considered the skills and strategies this program emphasizes and that they choose to ignore the solutions in favor of developing the mathematical processes and skills stipulated in the curriculum (Alberta Education, 2017). In her book Mathematical Mindsets, Boaler (2016) describes a similar activity where students are asked to partition a pan of brownies. When they are stuck, she asks her students to represent the mathematics problem as a drawing (Boaler, 2016). Boaler describes the value of representing ideas as “immensely helpful for students, both in school mathematical work and in life” (Boaler, 2016 , p. 185). Alternate forms of mathematical ideas, “graphs, tables, words, expressions, […] drawings and even doodles”, can act as road maps for students who are attempting to navigate concepts for the first time (Boaler, 2016 , p. 185). She reminds her readers that experienced problem solvers approach difficult problems from multiple points of view and regularly start from scratch multiple times before finding success (Boaler, 2016). The paint jar task grants students the same opportunity as the brownie task when delivered on its own; a chance to explore a mathematical map that can be used to navigate the world of fractions (Brydon et al., 2011b).
Create a problem about fractions.
The final problem in this sequence of mismatched operational problems invites students to create their own problem. However, over the course of this lesson there was no opportunity for students to engage in problem creation; at no point were students immersed in context, presented with a task that demanded them to create a mathematical expression, or placed in a position of power (Kokka, 2015; Meyer, 2014). The authors have crippled their student’s metacognitive processes by attempting to maintain control the entire time, never once bothering to help students become aware of the requirements of their learning processes (Alberta Education, 2017). The task of problem creation requires students to understand what information they need to resolve a problem, determine the level of achievement, the required rigor, and the completeness of the solution (Kokka, 2015). The proposed task, as it exists in this sequence of tasks, is a substitution exercise rather than a creative invitation (Henningsen & Stein, 1997). After being subjected to meaningless exercises and dictatorially mandated to solve problems using solutions that the authors have determined as appropriate it would not be surprising to find problems that mirror those found previously in the lesson with the numbers interchanged (Brydon et al., 2011a).
Sequencing.
It is not the tasks themselves that destroy the integrity of this lesson. It’s all the extra hints, projections, assumptions, and recommendations that make this resource inaccessible to students. Nelson Education seems to believe that students in the Math 10-4 program have a well-developed mathematical toolkit at their disposal. A decent lesson could erupt if one were to scrap the embellishments, cull the hints, and discard the recommended steps. Abandoning the notion that we can explore every mathematical operation in a single lesson and choosing a sequence of tasks that ranges from practical experiences to abstract exercises will be key to providing students with a valuable learning experience (Sullivan et al., 2009). These four tasks could serve the purposes of the curriculum with little effort. The cinnamon bun problem introduces students to the concept of fractions and allow students to recreate contexts concretely and pictorially. The paint problem leads students to experience alternate mathematical solutions such that they open their minds to a variety of acceptable mathematical content. The numerical problems belong next in the sequence so that students might consider how measurement approaches are related to abstract operations and procedures. Finally, those students who are inspired could be asked to create multiple problems of various difficulty levels and to describe the qualities that make their problems worth exploring (Davis, 2001). I am confident that students who encounter this sequence of tasks in a supportive environment with a knowledgeable instructor would realize the essential components in the program of studies.
Conclusion.
I have attempted to introduce readers to appropriate changes that can be made to the tasks provided by Nelson Education and to recommend experienced educators from whom we can learn valuable lessons regarding task construction and execution. These instructors recognize that the approved textbooks do not necessarily represent the most effective methods of imparting the curriculum and undertake massive efforts to empower themselves pedagogically. Among these instructors are Catherine Humphreys, Dan Meyer, and Jo Boaler; educational superstars striving to bring valuable learning experiences to students internationally. I encourage teachers to abandon the highly procedural methods that traditionally accompany the instruction of the division of fractions and encourage them to adopt the collective resources available publicly from these instructors. Finally, I have suggested a potential sequence of tasks from the Nelson Education resource that could be used for teaching the division of fractions in recognition of the mass that weighs heavily upon teachers who are burdened by excessive teaching loads.
References
Alberta Education. (2017). Knowledge and employability mathematics 10-4, 20-4. Retrieved from https://education.alberta.ca/media/3653319/kemath1020.pdf
Boaler, J. (2016). Mathematical mindsets: Unleashing students’ potential through creative math, inspiring messages and innovative teaching . (Kindle ed.). San Francisco, CA: John Wiley and Sons, Inc.
Boaler, J., & Humphreys, C. (2005). Connecting mathematical ideas : Middle school video cases to support teaching and learning. Portsmouth, NH: Heinemann.
Brydon, C., Desrochers, S., Grill, E., & Lisafeld, N. (2011a). Mathematics for apprenticeship and workplace 10. Toronto, CA: Nelson Education.
Brydon, C., Desrochers, S., Grill, E., & Lisafeld, N. (2011b). Mathematics for apprenticeship and workplace 10: Solutions. Toronto: Nelson Education.
Brydon, C., Desrochers, S., Grill, E. & Lisafeld, N. (2011c). Nelson apprenticeship and workplace. Retrieved from http://www.nelson.com/wncpmath/apprenticeship/about.html
Davis, B. (2001). Why teach mathematics to all students? For the Learning of Mathematics, 21(1), 17-24. Retrieved from http://www.jstor.org.login.ezproxy.library.ualberta.ca/stable/40248342
Henningsen, M., & Stein, M. K. (1997). Mathematical tasks and student cognition: Classroom-based factors that support and inhibit high-level mathematical thinking and reasoning. Journal for Research in Mathematics Education, 28(5), 524-549. Retrieved from http://www.jstor.org.login.ezproxy.library.ualberta.ca/stable/749690
Kokka, K. (2015). Addressing dilemmas of social justice mathematics instruction through collaboration of students, educators, and researchers. Educational Considerations, 43(1), 13-21. Retrieved from http://coe.ksu.edu.login.ezproxy.library.ualberta.ca/edconsiderations/back-issues.html
Meyer, D. (2014). Nana’s lemonade. Retrieved from http://www.101qs.com/3043
Morgan, C. (1996). “The language of mathematics”: Towards a critical analysis of mathematics texts. For the Learning of Mathematics, 16(3), 2-10. Retrieved from http://www.jstor.org.login.ezproxy.library.ualberta.ca/stable/40248208
Sullivan, P., Clarke, D., & Clarke, B. (2009). Converting mathematics tasks to learning opportunities: An important aspect of knowledge for mathematics teaching. Mathematics Education Research Journal, 21(1), 85-105. Retrieved from http://www.eric.ed.gov.login.ezproxy.library.ualberta.ca/contentdelivery/servlet/ERICServlet?accno=EJ883865
Appendix A: Nelson Education – Solving Problems with Fractions
Page 67, 7.
a) 5/8 ÷ 1/8 = 5/8 x 8/1
= ____, or ____
b) 1/2 ÷ 3/4 = _____ x _____
= ____, or ____
Page 69 Example 1
Aden is a baker. He cuts a 14 1/2 in. roll of dough into 1 1/4 in. slices for cinnamon buns. How many buns can he make from one roll?
a) What equation can you use to solve this problem?
Number of buns = 14 1/2 ☐ _____
b) Rewrite the equation using improper fractions.
Number of buns =
c) How many buns can Caden make from one roll?
Page 70. 3.
Kelsey has three jars of paint to pour into cups at a daycare. Each cup holds 3/10 of a jar. How many cups can Kelsey fill?

Page 71. 7.
Create a problem about fractions in a measurement situation that someone could solve by dividing. Show the solution.
Problem:
_________________________________________________________________________________________________________________________________________________________________________________________
Solution:
Appendix B: Dan Meyer – Nana’s Lemonade
Prologue:
Act 1:
How many lemon wedges should we use to make it taste the same?
What’s your guess?
What’s an answer you know is too high? Too low?
Act 2:
What information would be useful to know here?
Guess the volume of the larger cup.
Act 3:
Sequel:
How large would a cup be that would require an /entire/ lemon to keep the same lemon taste?
How many lemons is enough?
Appendix C: Cathy Humphreys & Jo Boaler – Defending Reasonableness
Appendix D: Jo Boaler & Alice Keeler – Color Coding Brownies (Modified)
Sam has made 6 pans of brownies. He wants to give 2/3 of a pan to each friend and share them with as many of his friends as he can. Partition the pans of brownies and use color coding to show how many of his friends will get brownies.