An Opportunity to Redefine
I think it’s interesting, the arrival of a student to my classroom. Closer to the beginning of the school year I might even suggest that they arrive at my classroom door full of excitement, ready to learn and explore, hoping it’s not just another school year. Those students arriving at my door have experienced years of failure; they’ve been passed along, assessed, diagnosed with learning difficulties and disorders, and evaluated. They often arrive at my classroom with an academic assessment as well, the RATT places them at between Grade 2 and Grade 6 level mathematical ability. They punish themselves verbally, physically, and psychologically having been convinced that they cannot participate in mathematical activities let alone participate in a manner they have defined as successful. The years of academic incarceration have resulted in the equivalent of a beat down; as if someone from Breaking Bad caught them selling drugs on their turf and decided to correct them. Here they are at the doors of my classroom expecting something different when out come the worksheets and out come the fractions as I encourage them to participate in group conversations and talk about how compound interest works.
Our relationships with students present to us intersections of classroom practice and humanity; opportunities to be a part of the authoring of the next part of their stories. The assumptions I make about my students, their skills, and their experiences within classrooms contribute to their continued or discontinued growth as individuals. My late night tinkering, enthusiastic innovation, and unsupervised self-accountability might either “support or suppress [student] participation” (Klein, 2007, p. 317). My behaviour, my choices, and the way I treat my students assigns to them a value and contributes to their desire to learn. My spontaneous remarks, personal relationships, and use of praise affect the quality of learning that occurs in my classroom. The structure of the school, the nature of the authorities present, the use of time, and the control of resources impacts individuals attempting to reform their narratives. Even my interpretations of educational mandates and the program of studies, and my use of various assessment practices can significantly impact a student’s learning trajectory (Apple & King, 1977)[1] It is at these intersections that I am obliged to pause and ask myself how my practices contribute to the bureaucratic nightmare that my students encounter while attempting to improve their educational outcomes. What “alienating effects” might my uninventoried, unaudited, unexamined and unaccountable classroom practices be proliferating (Klein, 2007, p. 317)?
Hopmann (1999) describes the conversations to be had as “a discursive set of uncountable possibilities in which all learning results which do not obviously contradict the frame set by discourse are legitimate events” (p. 95) Thus, I have an ethical responsibility to examine my classroom practices and the experiences available to my students inside my classroom within these discursive boundaries. Aoki (2005) describes the conversations that follow as messy, at best, and drives educators towards reflective practices that liberate practitioners from “unconsciously held assumptions and intentions that lie hidden”. Rationalizations, Aoki (2005) states, act as indicators of ideology; he recommends educators reaffirm their rationalizations of teaching practices through purposeful examination.
Aoki’s (2005) suggestions imply that our current rationalizations are a product of our times and that what is perfectly reasonable in this moment is driven by “the basics [… -] underlying epistemic, axiological, telic, and ontological bases”. For example, according to Aikenhead (2017) an“absolutist philosophy of education” has directed school mathematics and dominated Canadian curriculum conversations since the mid-nineteenth century. Mathematicians and mathematics educators like myself often sanction these philosophies and consequently participate in practices that marginalize at-risk populations (Aikenhead, 2017). In this paper, the assessment practices that I use in my own classroom take center stage; I revisit my current assessment practices, recognize influences that have led to them, concede their positive and negative attributes, take responsibility for their rationalizations, and acknowledge the impact they have had on student learning. I am encouraged by the thoughtful use of a variety of practices by educators in Alberta classrooms as I raise issue with my own practices and reexamine their legitimacy. In an effort to respond intentionally to narratives of my students and their pleas for renewed curricula I attempt to reimagine assessment as an evolved teaching practice that helps to make room for enhanced school experiences for all students. Alas, I fear that these ponderings leave me with far more questions than I start with, and far fewer answers, as I repeatedly remind myself to return to this central issue: How do I continue to contribute to the marginalization experienced by my students?
A Problematic Classroom Practice
Devlin (2000) suggests that students just need to want to do mathematics. Yet teachers steadfastly hold to their monotone programing and their claims that their programs represent better ways to learn mathematics. For example, Apple’s (1977) kindergarten teacher justifies her classroom activities “in terms of the preparation of the children for elementary school and for adulthood” (p. 353). “You give them positive feedback. Even if they get it wrong, they are not scared to give an answer” another teacher states as they justify yet another teaching practice (Klein, 2007, p. 317). My own practices are justified in a similar manner; I perpetuate my own values without asking what is it that students need. I use tools in my classroom claiming that they provide students with a concrete foundation for the study of indirect measurement and that “all the little marks on the rulers and protractors lend them authority [… and] a sense of autonomy”[2]. Or when I justify spending our time in class learning, talking, counting, drawing, measuring, building, and playing” and limit high-stakes assessment practices in my classroom to “one, singular, exam at the end of the course”[3] to boost learning outcomes. While our criticisms might easily be directed at an instructor, Schwab (1973) assigns critics the responsibility of directing their “[scrutinous eye towards whether a practice] should be imposed upon a student by way of the curriculum” (p. 507).
Perhaps most commonly practiced, certainly practiced by myself not too long ago, are grading procedures dominated by averages. Analogously, the material assigned by a teacher can be represented by a circle.
As students complete a course their progress is reflected in their grade. Portions of the circle are shaded in as assignments are completed and assigned grades through grading schemes chosen and used by instructors. Educators assign various weights to the assigned tasks, rationalizing each assigned grade and the weight of each task as they proceed through the mandated outcomes. While offering educators an easily justified grading opportunity, this method of grading encourages students to fight for an extra mark or two as they participate in a limited number of tasks as they are forced to compete in mundane competitions that educators refer to as exams. They pander to those in power for marks that raise their averages and fight for an image that sustains their sense of pride; they earn their spot from educators who award social standing. Percentages assigned by instructors for tasks are flashed around like cash and project students into various career paths with little concern for the consequences and barriers faced by the participants as a result of the decisions that are made.
Various rationalizations have led to assigned weightings of up to fifty percent for standardized assessments by those who are “granted the right to dispose of the standards of public education” in Alberta (Hopmann, 1999, p. 102). Responding to “discussions with students, teachers, parents and school boards” in 2015, Progressive Conservative Education Minister Gordon Dirks rationalized changes to the diploma examination “weighting regime” saying:
“A single examination cannot assess all the strengths or weaknesses of a student, even on a single topic. A single exam mark, weighted at 50%, does not allow students who may have greater difficulty writing high-stakes exams or who are undergoing unique stresses on the day of the exam, to fairly excel,” (Dykstra, 2015)
Dirks claimed that changes to the weighting “may even increase high school completion rates or post-secondary acceptance rates” though not everyone is yet convinced of the advantages of the changes (Dykstra, 2015). The current United Conservative Party intend to return to “a 50/50 split between Diploma grades and school grades for grade 12” but has since “ put that on hold” (French, 2019). Concerned students who voiced their opinion at the Speak Out 2012 Conference said that these high-stakes exams helped “prepare students for the future by having them deal with stress [… , holding] teachers to a high standard, [… helping] maintain Alberta’s strong reputation in education” and “[motivating] students to learn the material “ (Government of Alberta, April 13-15, 2012, p. 1).
However, Lia Daniels, from the University of Alberta, said she “can’t think of a course in her faculty where the final exam was worth more than 40 per cent” and calls into question the necessity of exposure to stress (French, 2019). The disadvantages quickly began to balance the advantages as students brought forth concerns about fairness, equity, format, monetary cost of preparation, and accessibility and language barriers (Government of Alberta, April 13-15, 2012). Ben-Yehuda, Lavy, Linchevski, & Sfard (2005) conclude that “common assessment tools, such as the school grades and diagnostic instruments used in preparing […] school files, have too little differential power to be useful” (p. 219). Evidence from Ben-Yehuda et al. (2005) offers that standardized assessments fail to account for individual differences, discourage students from participating in mathematical discourse, set students on deteriorating trajectories, and “diminish their chances for effective intervention” (p. 219). Students can become afraid to participate much like “Mari [who] refused to show how she counted fingers [believing that] counting fingers was [contrary to] proper arithmetic behavior” (Ben-Yehuda et al. 2005, p. 183).
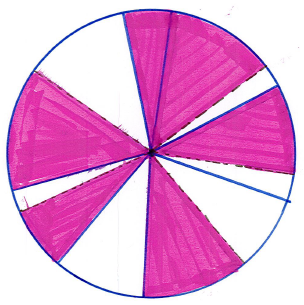
Daly (1967) indicated that “parts of the mathematics program” have been used as rationalization for those University administrators granting admission to “screen and prevent “lazy and stupid students” from entering University” institutions since 1925 (Daly, 1967, p. 11). Standardized assessments have also lead to “a hierarchy of ‘good’ and ’bad’ schools […] in relation to [what is being measured]” and distinguishes this knowledge from that knowledge which isn’t measured. (Hopmann, 1999, p. 102). Discussions about fairness have prompted students to share detailed accounts of their own strategies during diploma examinations and similarly, prompted exam administrators to respond to concerns of cheating, most recently in 2018 (Tupper, 2010). These concerns return me to the analogy of the circle:
We use our fears of cheating and fairness to rationalize a substitution of examinations; anyone familiar with exams is already familiar with this idea. Exam administrators use “a statistical process called equating, or linking, [to adjust] for the differences in examination-form difficulty”, rationalized by the claim that exams are fair if the difficulty of the exam is maintained ie. if 30% of students are able to successfully respond to a problem it is replaced with another problem that 30% of students are able to respond successfully to (Alberta Education, 2018, p. 12).
The various ethical arguments for or against the substitution of individual problems on standardized exams lead us now to a discussion of linking with respect to the substitution of entire curriculum items having now established that educational institutions have previously approved of such rationalizations (Alberta Education, 2018). When might it be fruitful to replace an entire final examination, whichever format is currently being used, with a final interview as Martin (2019b) has? “What happens at the final?” Dave asks,
“I have yet to see a coach sit silent on a bench on the final tournament game. […] In my high school classes I’ve successfully pushed the envelope as far as, I removed the final exam. Even AP calculus classes, even diploma classes, no final […] students had to convince me in an hour, talking to me, that they mastered the top ten ideas that we learned that year. […] I learned more about a kids understanding in sixteen minutes of conversation than I ever did in a four hour test. […] I had kids coming to my final excited, proud because they were going to show off things they had created” (Martin, 2019b).
Certainly there is some merit to this. Martin (2019a) recalls his move from item-based assessments (ie. multiple choice and written response) to outcome-based assessment in 2013 in his efforts to “challenge the grading system” (p. 26). Martin (2019a) encourages teachers to “only assess in a way that increases learning”; in his classroom, students “showcase [their] skills, knowledge or ability to work”, and “learn from their […] exams” as they participate in conversations about the material with their instructor during their final assessments. While this might draw the attention and critique from those not prepared to address the concerns of stress and readiness raised by students (Government of Alberta, April 13-15, 2012, p. 11), it is far closer to Schwab’s (1973) emphatic enthusiasm for “material […] used in the service of the student” (p. 15) and enthusiastically embraced by parents and students alike (Martin, 2019a).

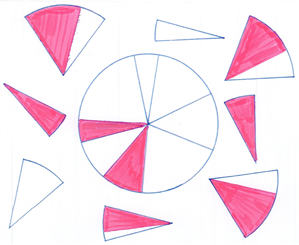
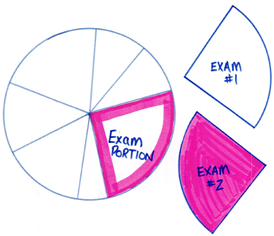
Further, Daly (1967) imagines a mathematics program in which “each student would be allowed to explore, to some degree, his own particular needs even for a large part of the time, [… a program where students] might never have to write departmental exams” (p. 14). In such a program, do we mandate content as suggested by Figure 1 or do we engage students in open conversations and explorations of the available learning opportunities as in Figure 3? Should recommended course material be provided to students as in Figure 4 as they wrestle with the ideas and concepts they choose to engage with and fulfill course expectations? Were a student to demonstrate mastery of the expected achievement outcomes by means other than a final exam, would one yet be necessary? Or should students be required to pass a final exam as my own educational institution’s assessment policy requires (Personal Communication, October 9, 2019)?[4] In hindsight, I wrestle with the lost learning opportunities that I have traded to make room for standardized assessment in my program. Simmt (2010) reminds us that we hold power over the practices that determine the narratives that students carry out of our classrooms. While there might not be a ‘right’ way to assess, Clarke, Clarke, & Lovitt (1990) assert that “it is through our assessment that we communicate most clearly to students which activities, […] learning outcomes” and, I suggest, which students, “we value most” (p. 118).
The Dissemination of Legitimacy
It is tempting to believe that there exists a global solution to our difficulties within “a static but unified body of certain knowledge” waiting to be dispersed among the masses (Aikenhead, 2017, p. 85). Equally as unnerving would be to suggest that the time we spend in school is sufficient to “catalog all the mathematical operations we perform as adults” in preparation for adult life (Kliebard, 1975, p. 34). This belief offers the promise of security, control, and a path to an improved quality of life for millions of people; alas, our reality is often less than ideal (Aikenhead, 2017). These alluring ideologies dominate the curriculum field and seize imaginations by anonymizing knowledge and erasing history (Gutiérrez, October 1, 2017). Gutiérrez (October 1, 2017) calls into question this erasure of humanity from classrooms. She claims that our “overreliance on any single knowledge” (p. 5) has led to tunnel vision among practicing educators and that the “predictive, generalizable, reductionist, and quantifiable” practices of mathematics educators referred to as “Western” (p. 5) misrepresent the whole of knowledge available to students through the practice of mathematics.
As such, there is a constant back and forth between school mathematics and society; a sustained marginalization of populations that rests upon the “valuing of ‘right’ answers”; an entire civilization searching in vain for “answers to its problems” and “leveraged by the ideology of quantification” (Aikenhead, 2017, p. 83). Kliebard (1975) acknowledges that the well-meaning curriculum of days past does little to encourage dialogue, “examination, analysis, and adaptation” of teaching principles (Kliebard, 1975, p. 34). Rather, these curricula have focused on previously encountered difficulties and “the solutions of […] which the race has devised up to the present moment” (Department of Education, 1924, p. 3). Ben-Yehuda, Lavy, Linchevski, and Sfard (2005) discuss the widespread “practiced abuses of literate mathematical discourse” and suggest that school walls inhibit mathematical communication, delegitimize mathematical content, and bar students from participation in valuable conversations (p. 176). These discourses, still wide-spread in my own classroom, invade our relationships, encourage the development of hierarchies, and depreciate valuable mathematical forms. Ben-Yehuda et al. (2005) caution educators about the banishment of colloquial mathematics from the classroom and its “destructive effect on those who consider themselves doomed to social exclusion” (p. 220).
To what end are educators trying to preserve this Platonist idealism? Apple & King (1977) suggest an elitist class sanctions a “social privilege, interest, and knowledge” dissemination responsible for maintaining the structures of educational institutions (p. 345). From within this structure, teachers act as weight bearing studs “encapsulated” by the political, social, and bureaucratic institutions of the day and “[re-produce] the problems that [they] are confronted with” (Apple & King, 1977, p. 355). Even scholars act to maintain the status quo; valuable discursive conversations are described as debates where “combatants” are pitted against one another and streams of knowledge such as inquiry and rigour and are weighed against one another, as though one could determine the value of either without acknowledging the ends served by each (Saskatchewan Bulletin, 1971, p. 1).
These Platonist structures condemn those populations who would be better served by teaching practices deemed as less valuable, in Canada no less than “eliminat[ing] or “socializ[ing]” unwanted racial or ethnic groups or their characteristics”; akin to cultural genocide by way of residential schools (Apple & King, 1977, p. 345). In Alberta, one would be hard pressed to find someone who couldn’t recall a series of regularities they experienced in school, my own perceived regularities included, that were unwarranted and uncompromising. Even I have often foregone any “non-linearity, subjectivity, experience, and intuition” in favor of teaching practices that consist of a single narrative: go to class, take down notes, memorize knowledge, complete homework, write exams, receive feedback, attend more classes, etc. But the recommended procedures and avenues have seldomly lead to the desired outcomes (Howe, 2013).
Donald (2019) suggests “that our knowledge and worldview would be greatly altered” if we were to remember what we forgot (p. 11). We might embrace the “context, the whole, and [the] relationship” (p. 123), strive to make “the learning of mathematics inviting or at the very least non-intimidating”, and see “the desire for certainty dissolved in a recognition of inevitable ambiguity” (Russell & Chernoff, 2012, p. 123; Davis, 1997, p. 375). We need to confront the “cultural fundamentalism” that Donald et al. (2011) frame as responsible for the powerlessness felt by teachers (p. 76). We need to engage in a dialogue that “brings forth a world of significance” rather than blindly subscribing to ‘best’ teaching practices. “Honouring and respecting the relationships we are enmeshed in” acknowledges the validity of our current existence while simultaneously re-exposing the ‘commonsense’ (Apple & King, 1977; Donald et al., 2011, p. 80). In doing so, “the good [our curricula] is supposed to do” can be realized and our students might be persuaded to continue their relationship with a subject they were once convinced was not for them (Schwab, 1973, p. 521)
An Ethical Responsibility
Consequently, I return to the grading schemes, substitutions, and analogies filled with circles only to discover that we live in a state of untruth. For the classroom practices we use today and the rationalizations used to justify them are ensconced in the tradition of tomorrow, “preserving the tried and true values of the society” (Kliebard, 1975). To “overcome meritocracy, disenfranchisement, and structural violence”[5] in the field of mathematics we must be willing to participate in dialogues of value. We must conquer our arrogance and examine our value-laden classroom practices even as our friends are complaining that they are “still marking… baaaaaah!” on social media (Personal Communication, November 17, 2019). Stakeholders vie to convince us that our classroom assessment must buy into a Platonist worldview, that these ideas are immutable, fair, and that these ideas are the best ideas. Our “value-governed” assessment practices have assumed those “legitimate knowledge[s]” that are espoused as the best way, the way that everyone should, the common-sense way (Apple & King, p. 344). For the sake of our students it is time to consider whether or not it is our current practices or whether it is our alternatives that indicate to our students the true value that we hold for them and adopt the classroom practices that do so.
Schwab (1973) emboldens his readership in an examination of “each statement of value or desired intention [as it] ought to evoke consideration of students […] as they are known or thought to be, with speculations on how they arrived at that desirable or undesirable condition” (p. 519). It is therefore our ethical responsibility to call out the “specialism”; the assumption that our practices are mainstream, well-examined, and deserving of automatic acceptance simply because they have been experienced by us and we didn’t turn out all that bad (Schwab, 1973, p. 519). To explore the impact of our school assessment experiences and the influence they’ve had on the activities in our own classroom is to invite “a measure of humility and shame”, a necessary ingredient, Schwab (1973) says, in practicing defensible curriculum (p. 520).
Considering this then, for a moment, I can imagine that any single assessment practice might never sufficiently account for the multitude of student experiences entering my classroom. And choosing thusly between assessment practices has “implications for those students […] who are caught in the middle, those being bounced from teaching and learning strategies of one camp to the other” (Russell & Chernoff, 2012, p. 116). Rather, we are obligated to participate in the “experiential continuum” of each student (Dewey, 1939, p. 10). In accordance with Dewey’s (1939) assertions of experience I suggest that in choosing assessment practices we must consider the effect of those practices on individual students. For it is with discretion that I might recommend an assessment experience that could leave “a [student] arrested on a low plane of development, in a way, which limits capacity for growth” or in a situation that renders them averse to further experiences (Dewey, 1939), p. 12). Failure to adapt such assessment experiences to the “needs and capacities of individuals” can result in “physical truancy [… and] an emotional revulsion against the subject” (Dewey, 1939, p. 17). Meaning, during the employment of classroom assessment practices “the future has to be taken into account” (Dewey, 1939, p. 17). For the learning experiences of our students must not conclude when they leave our classroom as they hand in their final exam and therefore no assessment practice may be dismissed unilaterally. Instead, Dewey (1939) suggests that we consider how curriculum experiences such as assessment might contribute to “the most important attitude that can be formed: the desire to go on learning” (p. 18).
Appendix A: Assessment Policy (Personal Communication, October 9, 2019)
- A variety of assessments (i.e., projects, written assignments, portfolios, presentations, quizzes, exams) are used.
- Class time will be provided to help students prepare for exams (i.e., reviews, study plans, practice questions.)
- All core subjects need a final exam, and students need to pass the final exam in order to pass to the next level. If a student passes the course work, but does not pass the final exam, it is the teacher’s responsibility to meet with the principal to discuss options.
- All exams must be supervised at all times by a teacher or teacher assistant.
- Provide accommodations and testing strategies listed in the Individualized Program Plans.
- If extra time is provided for an exam, it is up to the teacher to determine how the exam is administered to prevent students from returning to previously exposed questions. Examples include:
- Arranging for the student to work into the next block
- Arranging for the student to work at lunch, during breaks, or after school
- Arranging an alternative, supervised area
- Breaking the exam into different parts so it can be administered over a few sittings
- If accommodations (i.e., extra time, alternative monitored space) are provided, please indicate on the progress report.
References
Aikenhead, G. S. (2017). Enhancing school mathematics culturally: A path of reconciliation. Canadian Journal of Science, Mathematics and Technology Education, 17(2), 73-140. Retrieved from https://doi.org/10.1080/14926156.2017.1308043
Alberta Education. (2018). Information bulletin mathematics 30–1. Edmonton, AB: Alberta Education.
Aoki, T. (2005). Towards a curriculum inquiry in a new key. In W. F. Pinar, & R. L. Irwin (Eds.), Curriculum in a new key: The collected works of ted T. aoki (pp. 89-110). Mahwah, New Jersey: Lawrence Erlbaum Associates, Inc., Publishers.
Apple, M. W., & King, N. R. (1977). What do schools teach? Curriculum Inquiry, 6(4), 341-358. Retrieved from http://www.jstor.org/stable/1179656
Ben-Yehuda, M., Lavy, I., Linchevski, L., & Sfard, A. (2005), Doing wrong with words: What bars students’ access to arithmetical discourses. Journal for Research in Mathematics Education, , 176.
Clarke, D. J., Clarke, D. M., & Lovitt, C. J. (1990). Changes in mathematics teaching call for assessment alternatives. Teaching and learning mathematics in the 1990s (pp. 118-129). Reston, VA: NCTM.
Daly, R. A. (1967). Alberta school mathematics, 1867-1967. Annual Publication of the Mathematics Council of the Alberta Teachers’ Association, 4(1), 4-14.
Davis, B. (1997). Listening for differences: An evolving conception of mathematics teaching. Journal for Research in Mathematics Education, 28(3), 355-376. Retrieved from http://www.jstor.org/stable/749785
Department of Education. (1924). Programme of studies for the elementary schools of alberta. Edmonton, AB: J. W. Jeffery King’s Printer.
Devlin, K. (2000). The maths gene: Why everyone has it but most people don’t use it. London, Phoenix.:
Dewey, J. (1939). Criteria of experience. Experience and education (pp. 33-50). New York, NY: Macmillan. Retrieved from https://archive.org/stream/experienceeducat00dewe_0?ref=ol#page/n9/mode/2up
Donald, D. (2019). Homo economicus and forgetful curriculum. In H. Tomlins-Jahnke, S. D. Styres, S. Lilley & D. Zinga (Eds.), Indigenous education: New directions in theory and practice (pp. 103-127). Edmonton, Alberta: University of Alberta Press.
Donald, D., Glanfield, F., & Sterenberg, G. (2011). Culturally relational education in and with an indigenous community. [Indigenous Education] in Education, 17(3), 72-83. Retrieved from https://ineducation.ca/ineducation/article/view/73
Dykstra, M. (2015). Alberta education changes weight of diploma exams from 50% to 30% of a students final grade. Retrieved from https://edmontonsun.com/2015/03/16/alberta-education-changes-weight-of-diploma-exams-from-50-to-30-of-a-students-final-grade/wcm/7b2b8e33-a3b5-439d-a6e2-4ae55a609483
French, J. (2019). ‘We’ve heard concerns’: UCP pauses plan to make high school diploma exams worth 50 per cent. Retrieved from https://edmontonjournal.com/news/local-news/weve-heard-concerns-ucp-pauses-plan-to-make-high-school-diploma-exams-worth-50-per-cent
Government of Alberta. (April 13-15, 2012). Demystifying diploma exams. Paper presented at the Speak Out, 1-7.
Gutiérrez, R. (October 1, 2017). Living mathematx: Towards a vision for the future. Paper presented at the Synergy at the Crossroads: Future Directions for Theory, Research, and Practice, 2-26.
Hopmann, S. (1999). The curriculum as a standard of public education. Studies in Philosophy and Education, 18(1), 89-105. doi:1005139405296
Howe, E. (2013). Bridging the aboriginal education gap in alberta. (). Edmonton, AB: Rupertsland Centre for Metis Research. Retrieved from http://albertametis.com/wp-content/uploads/2013/08/RLI_Bridging_the_Aboriginal_Education_Gap_in_Alberta.pdf
Klein, M. (2007). How is it that learning mathematics in the early years can become so difficult? A post-structuralist analysis. Contemporary Issues in Early Childhood, 8(4), 313-319. doi:10.2304/ciec.2007.8.4.313
Kliebard, H. M. (1975). The rise of scientific curriculum making and its aftermath. Curriculum Theory Network, 5(1), 27-38. doi:10.1080/00784931.1975.11075792
Martin, D. (2019a). Differentiating assessment. Delta-K: Journal of the Mathematics Council of the Alberta Teachers’ Association, 55(2), 25-27.
Martin, D. (2019b). Engaging math learners & differentiating math assessment (S. Lawrence Trans.). Edmonton, AB: The ERLC Show.
Russell, G., & Chernoff, E. (2012). The marginalisation of indigenous students within school mathematics and the math wars: Seeking resolutions within ethical spaces. Mathematics Education Research Journal, 25(1), 109-127. doi:10.1007/s13394-012-0064-1
Saskatchewan Bulletin. (1971). “New math” sparks lively debate. Delta-K (Formerly Mathematics Council Newsletter), X(4), 1-2.
Schwab, J. J. (1973). The practical 3: Translation into curriculum. School Review, 81(4), 501-522. Retrieved from https://search.proquest.com/docview/1290901545
Simmt, E. (2010). The diploma exam and the role of communication in mathematics literacy. Delta-K: Journal of the Mathematics Council of the Alberta Teachers’ Association, 47(2), 12-16.
Tupper, L. (2010). Alberta education wraps up investigation of diploma exam cheating. Retrieved from https://edmonton.ctvnews.ca/alberta-education-wraps-up-investigation-of-diploma-exam-cheating-1.507681